Att förstå kunders avhoppsbeteenden är en central insikt inom kundhantering för företag som vänder sig till privatkunder. Med denna kunskap kan man både förstå bättre hur man kan behålla kunder längre men även vilka kunder som man bör koncentrera sin nykundsbearbetning på.
Läs mer om hur du kan dra nytta av avhoppsanalys här (Sju sätt att dra nytta av en churn analys).
Det är dock när avhoppsanalysen används som input för att beräkna ett kundlivstidsvärde som man får det ultimata måttet för att värdera olika kundstrategier mot varandra. Ett kundlivstidsvärde summerar kundens framtida förväntade engagemang och beror på det marginalen av förväntat engagemang multiplicerat med förväntad kundlivstid. Ett steg på vägen till kundlivstidsvärde är att få fram en uppskattad kundlivslängd från sin avhoppsrisk.
Churn eller avhopp beskrivs ofta som en procent som slutar under en viss period, en så kallad churn rate. Om ett företag till exempel har hundra aktiva kunder i början av en månad och två av dessa kunder slutar sitt engagemang så är procentuella avhoppen 2 % (två stycken av hundra). Det kan vara mycket givande att följa procentuella risken per månad som kund för att följa under vilka perioder och sammanhang som risken till churn är störst för kunderna. Procent är fortfarande svårt att förstå och för att verkligen förstå värdet av detta behöver man istället se vad churn rate innebär för en förväntad livslängd för kunderna. Med en förväntad livslängd i till exempel månader så närmar vi oss det optimala kundlivstidsvärdet.
Till detljerna
Hur får man förväntad livslängd från en procentuell churnrate? Ett enkelt sätt är att tänka sig att man summerar framtida sannolikheten att kunden fortfarande är kund och risken att kunden inte är kund beskrivs av just churn rate.
För att ta som exempel:
Säg att du har en churn rate per månad som är 4 %.
Första månaden är det 4 % risk att kunden hoppar av. Vi kan alltså räkna med att kunden har en sannolikhet att vara kvar efter månadens slut till 0,96 (1-0,04).
Nästa månad så är det igen 4 % risk att kunden hoppar av. Men nu börjar vi här inte säkert med att vi har en kund. Från förra månaden så har vi en sannolikhet på 0,96 och på denna har vi nu en 4 % risk att hoppa av.
Efter månaden har vi en sannolikhet till 0,96*(1-0,04)= 0,9216 kunden fortfarande är aktiv kund.
På detta vis fortsätter man att summera framtida sannolikheter. Denna summering kan enkelt göras med programmeringsscript men det går alldeles utmärkt att ställa upp i excel, då kan det se ut så här:
Tidshorisont
Exceltabellen ovan kan uträknas som att vi under tolv månader kan förvänta oss 9,29 aktiva kundmånader i medel per kund. En del kommer naturligtvis fortfarande vara aktiva efter tolv månader medans andra har hoppat av och blev bara kund en månad.
Det går ju dock att se att om man låter denna tabell gå vidare framåt i tiden så kommer det läggas på många fler månader. Med ett programmeringsscript så skulle man kunna traversera tusentals månader framåt men det vanliga är att man sätter en begränsning i någon typ av tidshorisont. Beroende på sin verksamhet kan den vara till exempel tio till femton år eller ännu längre om det rör sig om en kundrelation som sträcker sig ännu längre under normala fall.
Om man så här fortsätter summera den förväntade sannolikheten att kunden fortfarande är en kund så får man en summerad förväntad kundlivslängd. Att summera med script tar ju dock lite tid att ta fram, en snabbväg till en förväntad kundlivslängd är istället att använda sig av regler för hur man integrerar sannolikheten, då får man istället en formel som man kan snabbt köra i Excel:
=(1-CHURNRISKPERMÅNAD)^TIDSHORISONt/LN(1- CHURNRISKPERMÅNAD)-(1-CHURNRISKPERMÅNAD)^0/LN((1-CHURNRISKPERMÅNAD))
Där churnriskpermånad är medelrisken i per månad. Till exempel 0,01 om den är 1 %.
Tidshorisont är här antal perioder som man valt som tidshorisont. I övrigt är funktionerna sådana som funkar i Excel.
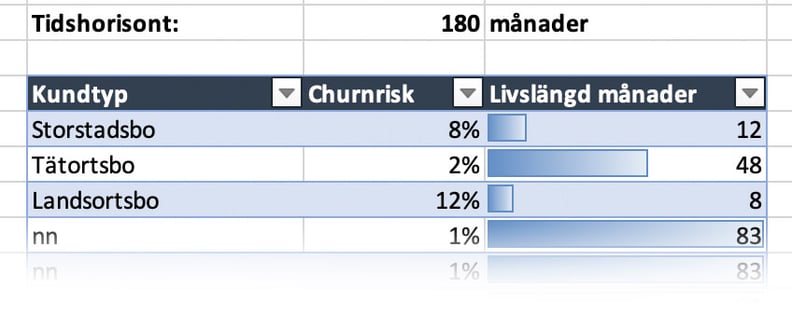
Med denna formel får man en snabb estimering av kundlivslängd och kan användas för att beräkna ett grundläggande kundlivstidsvärde. Perfekt för att påvisa skillnaderna mellan olika kundtyper och beteenden.
Om du vill veta hur man tar fram ett churn-risk så kan du läsa mer i denna artikel:
Så gör du en Churn-analys från grunden.
Fyll i din epost om du vill ha en kopia på Excel-filen från ovan exempel:
Sådan kommer du i gang
Da kundernes levetid er en af de vigtigste faktorer for en god forretning, er der utallige måder at drage fordel af churn-analysen på både i planlægningsarbejdet og rent driftsmæssigt. Disse syv er blot nogle få eksempler, der både kan opdeles i detaljer og udvides med flere. En god måde at komme i gang på er at starte med en eksplorativ analyse for derfra at bestemme, hvordan man med de laveste omkostninger kan komme i gang og bruge modellen til at forbedre forretningen.
